Introduction
In my previous post I made a neural network from scratch with the idea of using it for a tic-tac-toe agent. In this post I’ll go over the training process. My general intuition is to play each agent with all other agents twice, once for “o” and once for “x”. A reward function would decide what score an agent gets each game. The agents with top score progress to the next epoch, where they are cloned and mutated to fill the dropped out population.
The training setup
Playing an individual game
A function is necessary for playing 2 agents against each other. It returns the who’s the winner, the number of moves, and if the game is a disqualification. If an agent makes an illegal move, he’s directly disqualified. A draw returns a winner id of 2, which is neither agent.
@dataclass
class GameResult:
winner: int
dq: bool
moves: int
def play_game(
agent0: NeuralNetworkAgent,
agent1: NeuralNetworkAgent
) -> GameResult:
board = TicTacToeBoard()
moves = 0
for agent, agent_index, side in cycle([(agent0, 0, "x"), (agent1, 1, "o")]):
if len(board.get_valid_moves()) == 0:
return GameResult(winner=2, dq=False, moves=moves)
move_to_play = agent.get_best_move(board)
try:
board.play_move(side, move_to_play)
except ValueError:
return GameResult(winner=abs(agent_index - 1), dq=True, moves=moves)
moves += 1
if board.get_winner() == side:
return GameResult(winner=agent_index, dq=False, moves=moves)
raise Exception("Unexpected cycle termination.")
Reward function
The reward function will be used after playing a game to determine the number of points each agent gets. This is a simple version of it, which I’ll be using at the start. It’s inspired by football matches, but it has potential pitfalls here.
def reward_function(gamer_result: GameResult) -> tuple[int, int]:
if gamer_result.winner == 0:
return (3, 0) # agent 0 wins
if gamer_result.winner == 1:
return (0, 3) # agent 1 wins
return (1, 1) # draw
Playing a league (epoch of training)
A league plays all agents against each other for both sides of the board. The reward function determines the points earned from each game. The overall league result is returned by this function:
@dataclass
class LeagueResult:
points: list[int]
games_played: int
dqs: int
moves_counter: Counter[int]
def play_league(league_agents: list[NeuralNetworkAgent], epoch: int) -> LeagueResult:
points = [0 for _ in league_agents]
dqs = 0
games_played = 0
moves_counter: Counter[int] = Counter()
for i0, a0 in enumerate(league_agents):
for i1, a1 in enumerate(league_agents):
if a0 == a1:
continue
result = play_game(a0, a1)
moves_counter[result.moves] += 1
agent0_reward, agent1_reward = reward_function(result)
points[i0] += agent0_reward
points[i1] += agent1_reward
if result.dq:
dqs += 1
games_played += 1
return LeagueResult(points, games_played, dqs, moves_counter)
Training epochs
Putting it all together, the training algorithm takes key training parameters and performs the process of playing all agents against each other, rewarding the winners, and then cloning and mutating their copies for the next round.
def train_epochs(
league_size: int,
winners: int,
save_epochs: int,
max_mutation_magnitude: float,
save_folder: str = "saved_nn_agents" # not implemented
) -> None:
agents: list[NeuralNetworkAgent] = [
NeuralNetworkAgent(f"e0a{i}")
for i in range(league_size)
]
for agent in agents:
agent.mutate(max_mutation_magnitude)
epoch_cycle = 1
epoch = 1
while True:
epoch_league_results: list[LeagueResult] = []
for i in tqdm(range(save_epochs)):
league_result = play_league(agents, epoch)
epoch_league_results.append(league_result)
last_result = [(i,j) for i,j in enumerate(league_result.points)]
last_result.sort(key=lambda a: a[1], reverse=True)
top_n = last_result[:winners]
new_agents: list[NeuralNetworkAgent] = []
for i, _ in top_n:
new_agents.append(agents[i])
while len(new_agents) < league_size:
copy_index = random.choice(top_n)[0]
nn_copy = agents[copy_index].nn.copy()
nn_agent = NeuralNetworkAgent(
f"e{epoch}i{len(new_agents)}",
nn_copy
)
nn_agent.mutate(max_mutation_magnitude)
new_agents.append(nn_agent)
agents = new_agents
epoch += 1
plot_league_results(
epoch_league_results,
epoch_cycle,
league_size * (league_size - 1)
)
epoch_cycle += 1
input(f"Epoch {epoch} checkoint")
The parameters of this function serve the following purposes:
league_sizedetermines the number of agents in the league.winnersdetermine the number of winners to proceed and be cloned for the next epoch.save_epochsdetermines after how many epochs to save the current agents. The saving of the agents is also paired with providing graphs on the performance of the agents since the last save.max_mutation_magnitudedetermines by how much the weights and biases in the network can change when they mutate.save_folderdetermines where the agents are saved.
You may also notice the plot_league_results method. This method plots information for the performance of the league since the last save:
@typing.no_type_check
def plot_league_results(results: list[LeagueResult], epoch_cycle: int, games_played: int) -> None:
records = []
for i, c in enumerate(r.moves_counter for r in results):
for k, v in c.items():
records.append({"sub epoch": f"{i+1}", "moves": k, "count": v})
df = pd.DataFrame(records)
fig, axes = plt.subplots(1, 2, figsize=(12, 5)) # 1 row, 2 columns
sns.lineplot(x="sub epoch", y="count", hue="moves", data=df, palette="tab10", ax=axes[0])
axes[0].set_title("Number of moves in game")
axes[0].grid(True, linestyle="--", alpha=0.5)
axes[1].plot(range(len(results)), [r.dqs for r in results])
axes[1].set_title(f"Number of DQs from {games_played} played games")
axes[1].grid(True, linestyle="--", alpha=0.5)
axes[1].yaxis.set_major_locator(mticker.MaxNLocator(integer=True, prune=None))
fig.suptitle(f"Results after epoch cycle {epoch_cycle}", fontsize=16)
plt.tight_layout()
plt.show()
Training attempts
Premier League style
Since I thought of the league concept, I was constantly thinking of football games. Let’s set up the leagues to work like them and see what happens.
The reward function gives 3 points to the winner of a game and 1 point to each agent if it’s a draw:
def reward_function(gamer_result: GameResult) -> tuple[int, int]:
if gamer_result.winner == 0:
return (3, 0) # agent 0 wins
if gamer_result.winner == 1:
return (0, 3) # agent 1 wins
return (1, 1) # draw
The parameters of the training algorithm are these:
train_epochs(
league_size = 20,
winners = 3,
save_epochs = 20,
max_mutation_magnitude = 0.5
)
After 20 cycles, the results look like that:
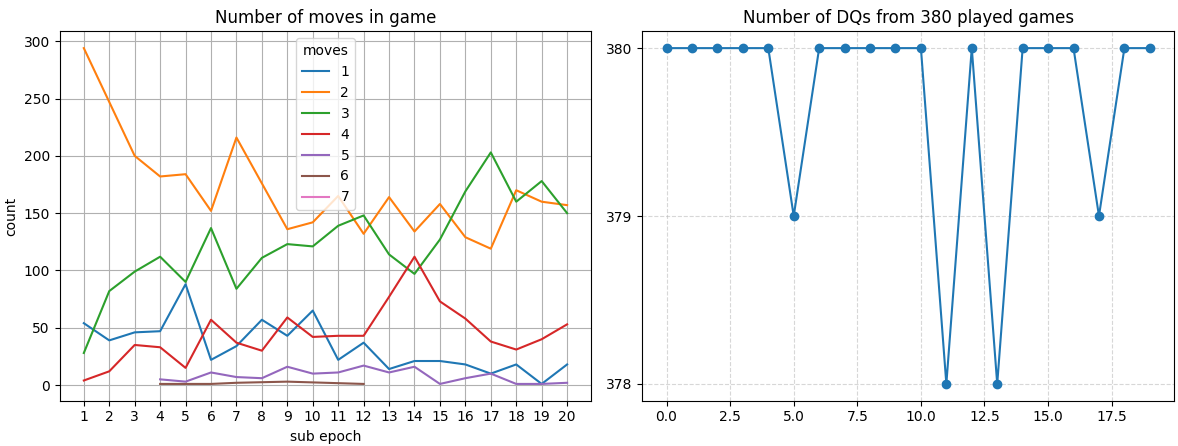The graph on the left plots the games’ move counts for each cycle. The y axis show the number of games played, the color represents the number of moves, specified in the legend. A trend of the agents being able to make more and more moves before being disqualified starts to emerge.
The graph on the right shows the number of DQs due to attempted illegal moves. At this stage of training, pretty much all games are DQs.
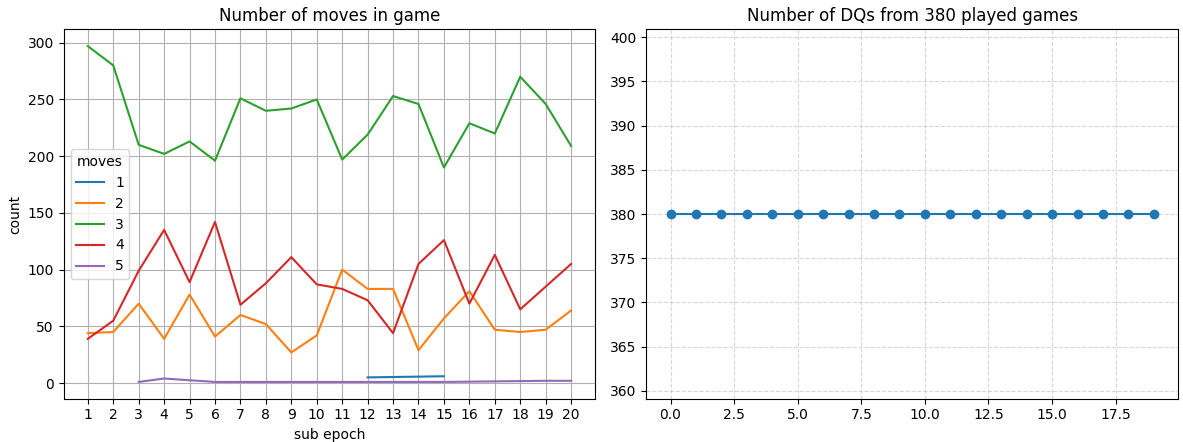After 100 epochs, most games have 3 moves, and there are a lot of games that reach 4. There’s not much improvement as a whole, however. We can also see that all games ended in DQ for the last 20 epochs. That’s not good performance.
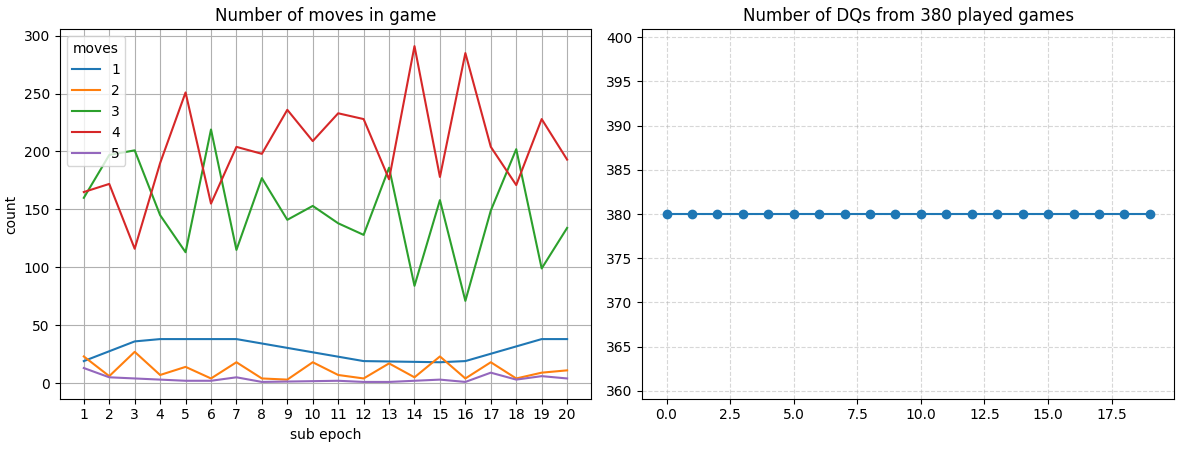After 570 epochs, the results look like this, an actual downgrade. During a point, after 200-300 cycles most of the agents were able to get to 5-6 move games, but then the model downgraded.
Increasing the agent pool
I feel like the previous approach fails due to the small pool of selected agents going to the next round. Even if an agent goes in the right direction, it’s very easy to drop off right after.
Keeping the reward function the same, I’ll increase the agent pool to 100 agents in a league. 50 of them will be winners. The idea is that there will be more focus on removing agents that are consistently bad.
train_epochs(
league_size = 100,
winners = 50,
save_epochs = 20,
max_mutation_magnitude = 0.5
)
After 20 cycles, the results are as follows:
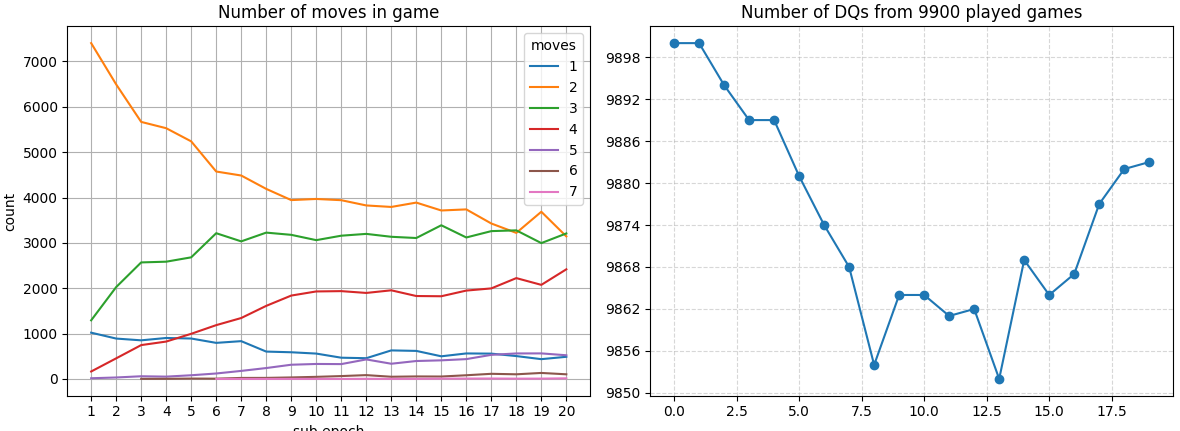It can be immediately seen that increasing the population makes the training results more smooth.
After 40 cycles, a clear trend of DQ reduction starts to form:
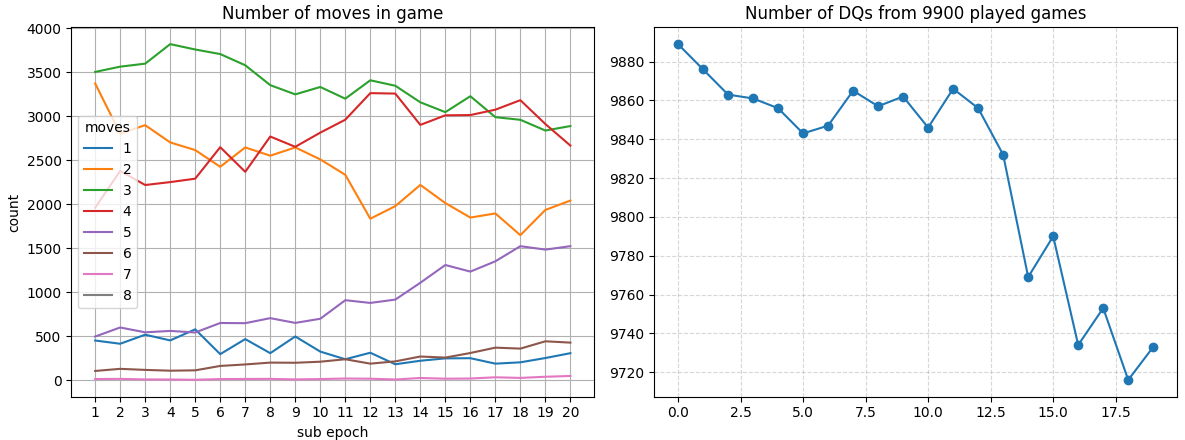
After 60 cycles, the trend keeps going:
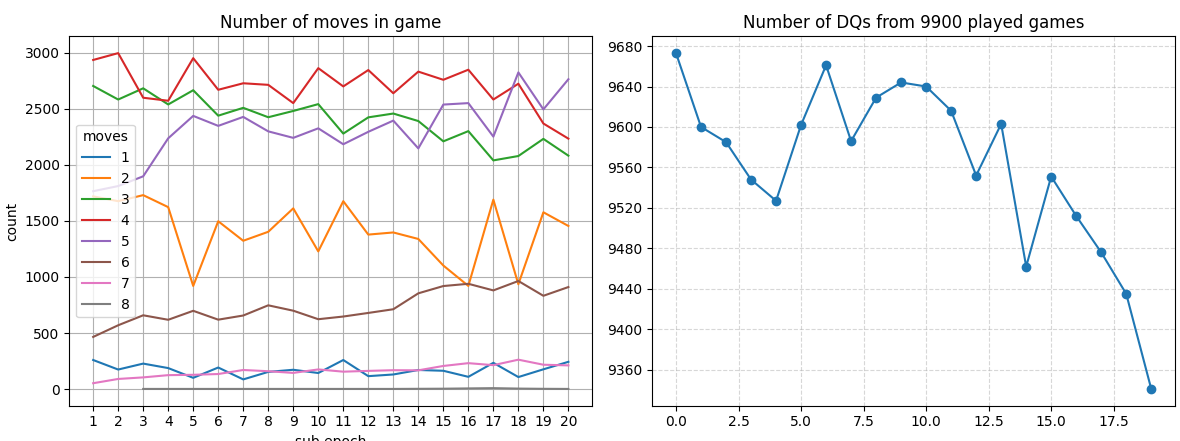
After 80 cycles, about 10% of the games aren’t DQ!:
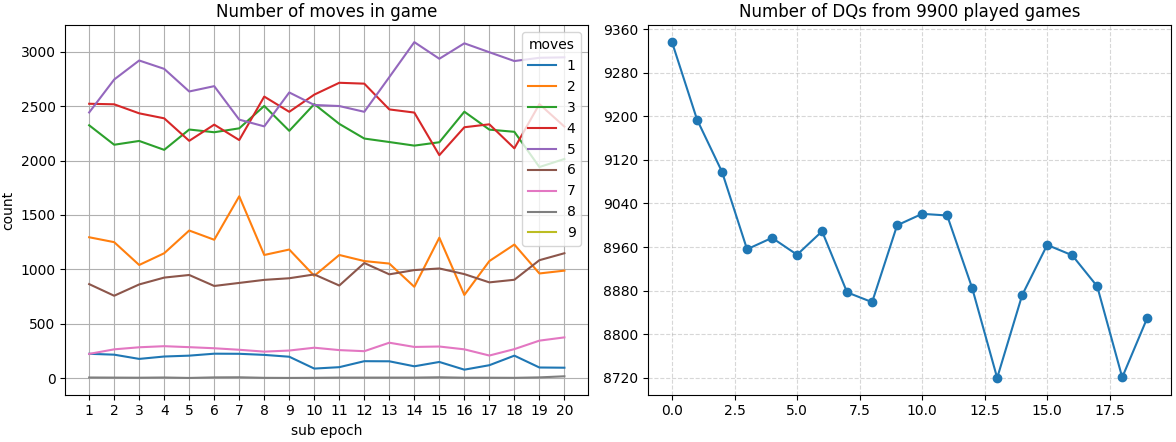
However, after 160 epochs, I got the following result:
There were some gains, about 20% of the games weren’t a DQ in one epoch, but the agents started to regress.
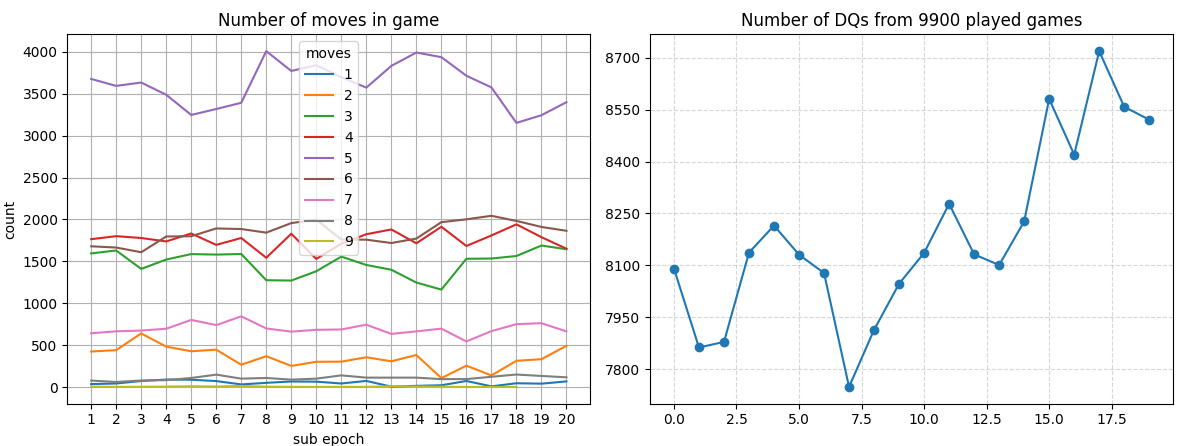
At this point I started to notice that the agent would regress a bit, and then progress again. The graph was only showing local extremes that weren’t useful to the training process as a whole. Because of this, I decided to make the graph encompass more epochs and train a new model so progress could be observed more broadly.
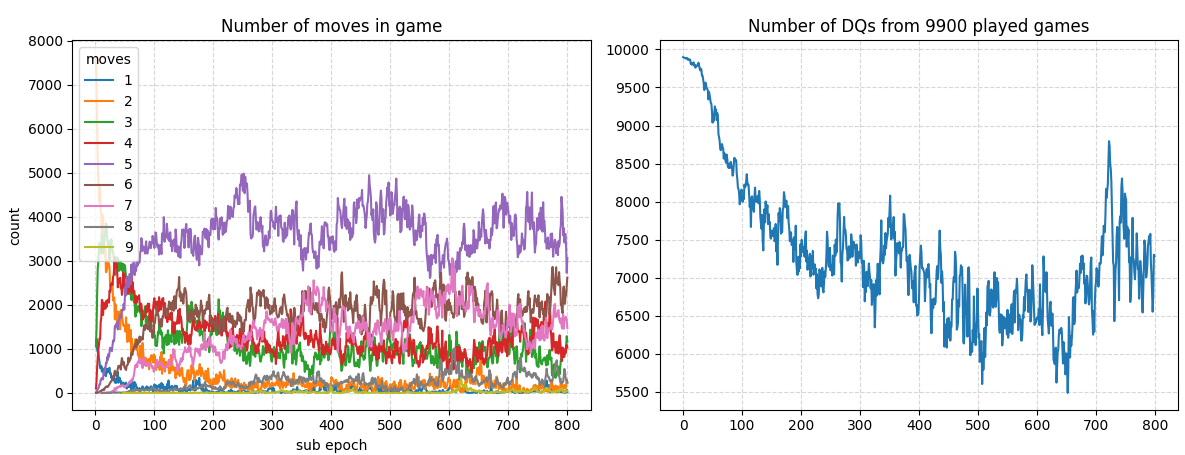This is a graph of 800 epochs of training. At one point almost 50% of the games were valid. I feel like this model has potential for nice results, but the current code is very slow to execute and I don’t have patience for thousands of epochs. The 800 epochs from above took about 30 minutes.
Punishing invalid moves
Maybe instead of just waiting for the agents to randomly adapt into doing the right move, we can encourage them by heavily punishing disqualification moves.
def reward_function(gamer_result: GameResult) -> tuple[int, int]:
if gamer_result.winner == 0:
return (1, 0) if not gamer_result.dq else (1,-10)
if gamer_result.winner == 1:
return (0, 1) if not gamer_result.dq else (-10,1)
return (1, 1)
The reward function now heavily punishes doing DQs. I also made a win worth 1 point. A draw should result in equal points, as perfect tic-tac-toe games are always a draw.
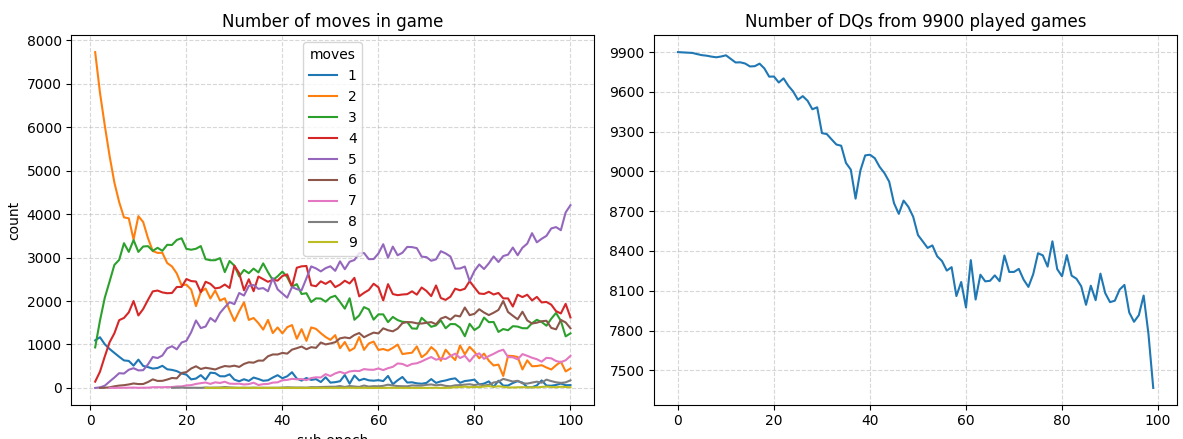After the first 100 epochs, 25% of the games played by the agents are actually consisting of valid moves.
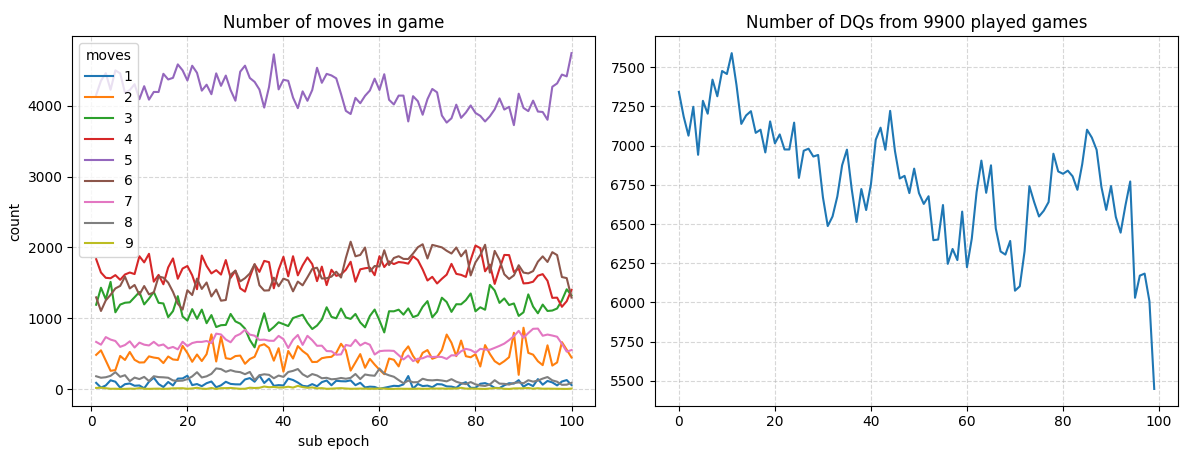At the 200th epoch, this method already beats the best results from the previous approach.
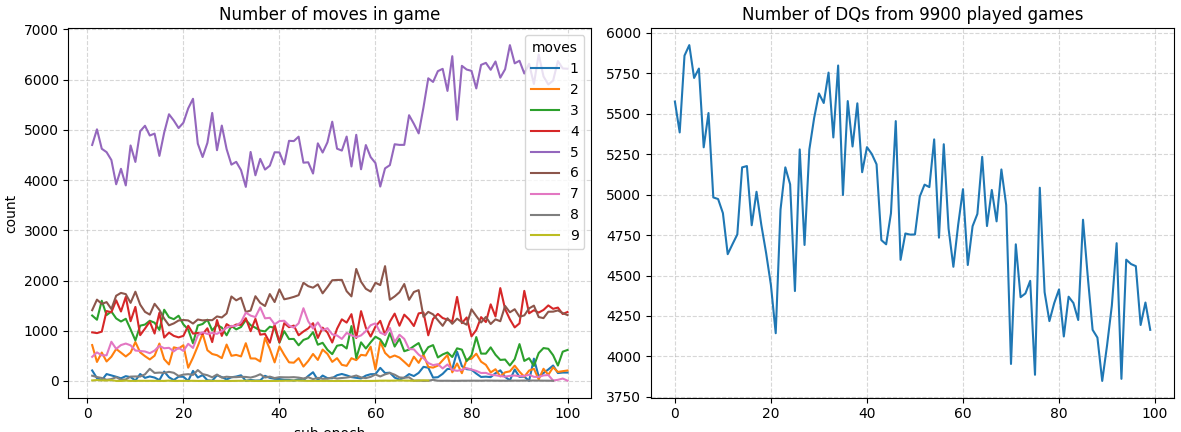After the 300th epoch, more than 60% of the games are valid. That’s significantly better than the last training approach. The big spikes look concerning, if they persist, I’m thinking of reducing the mutation magnitude for the biases and weights in the networks.
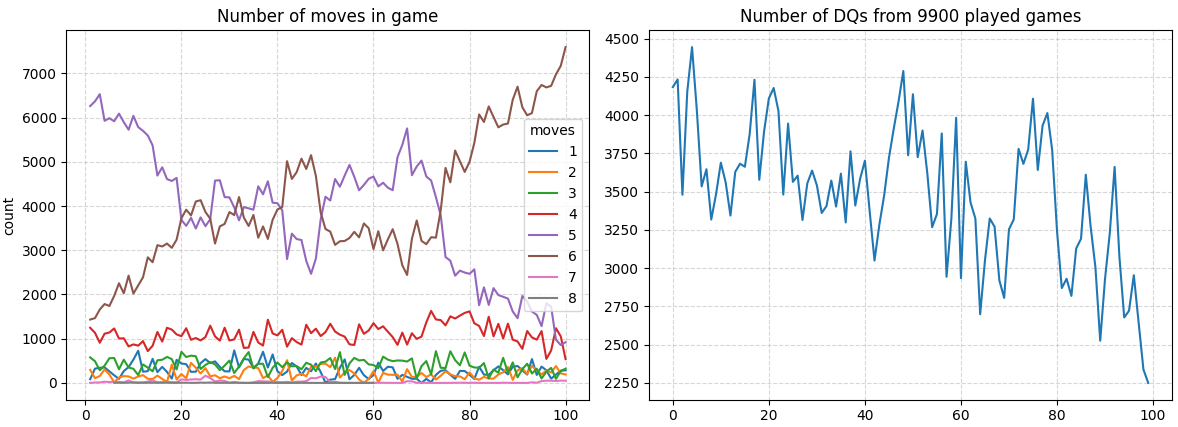Epochs 300-400 bring further significant improvements to the performance of the agents. For some reason agents start getting stuck on playing 6-move games.
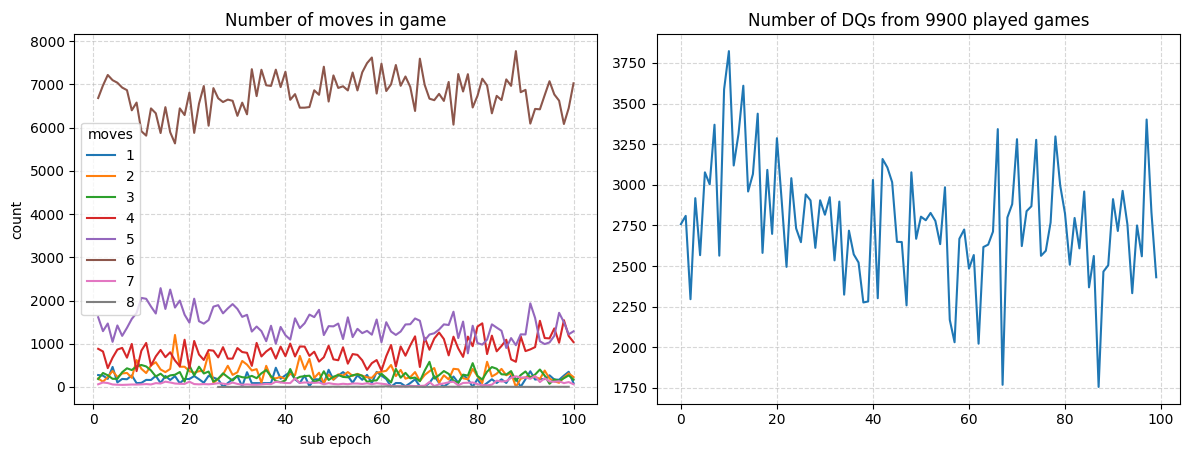Epochs 400-500 the agents look really stuck on whatever 6-game move they’re playing. At least a point is reached where more than 80% of the games are valid.
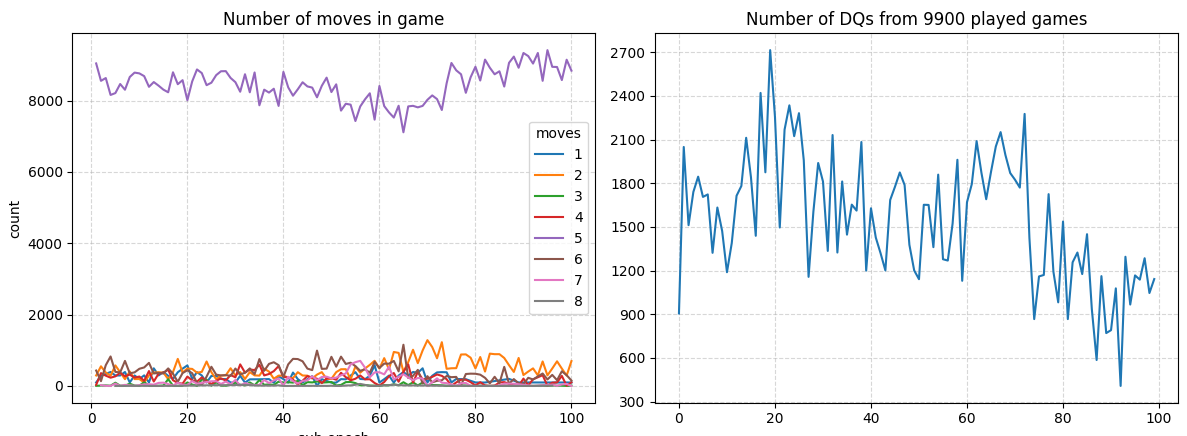Epochs 700-800 less than 10% of the games end because of DQ. The agents may soon start to actually play the game correctly.
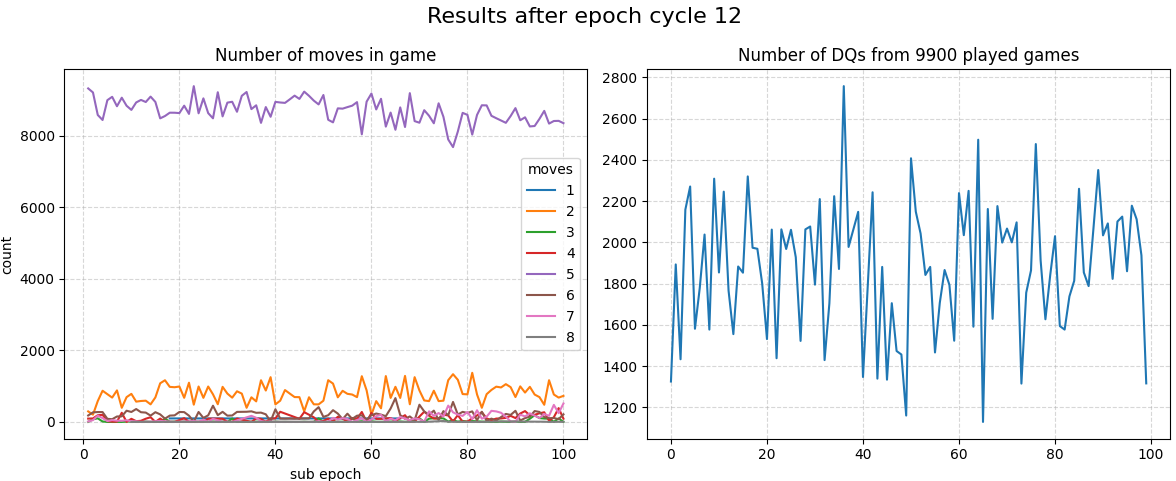Epochs 1100-1200 the number of valid games start to get very spiky. There’s also a resurgence of 2-move games.
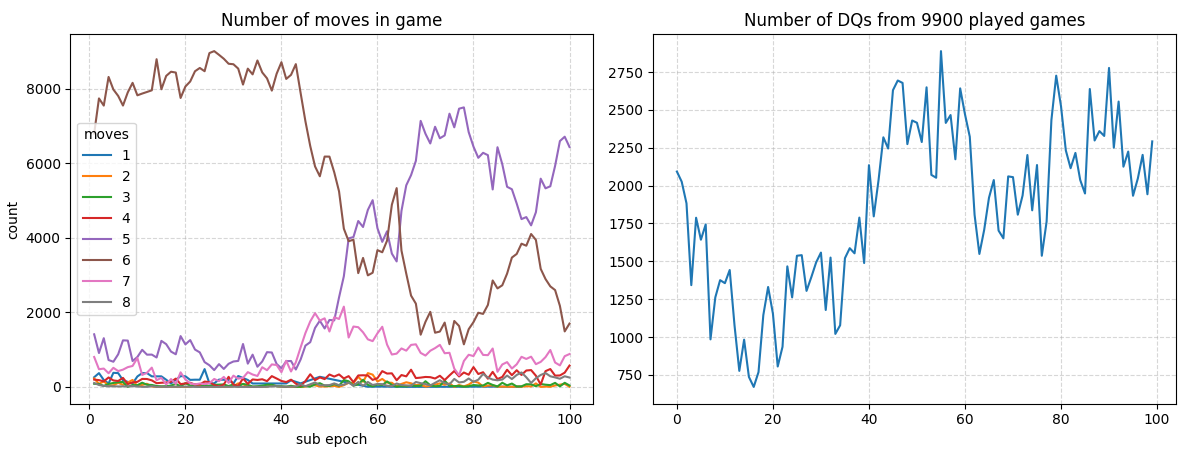Epochs 1700-1800 there was the same reversal pattern. At this point I’m thinking of trying something new.
Reducing the neurons
I removed the hidden layer of 15 neurons, now the inputs go directly to the output 9 neurons. I also reduced the max mutation magnitude to 0.1 and reduced the number of winners to 25. I can immediately see that training happens much faster now.
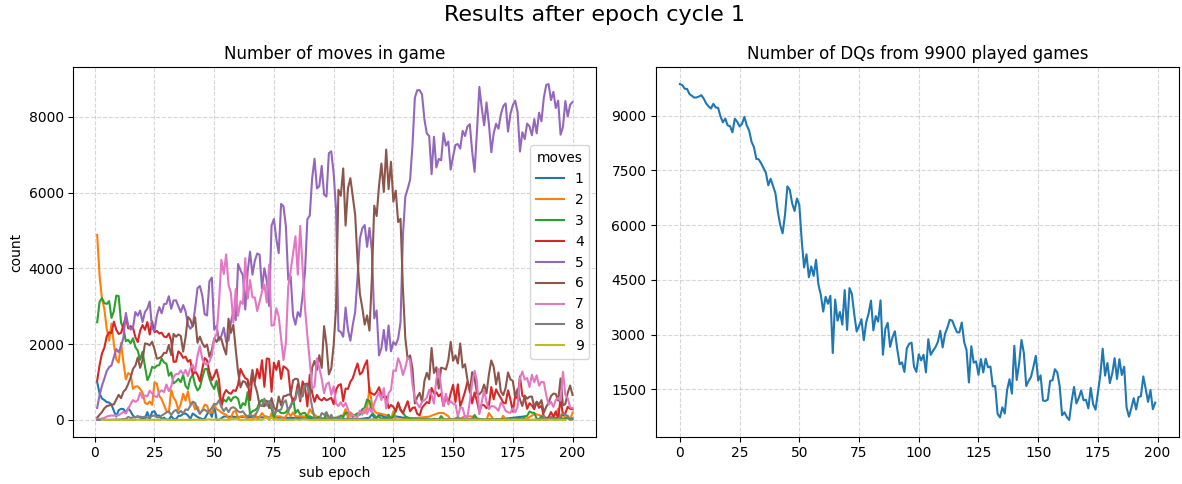Epochs 0-200 show promising results.
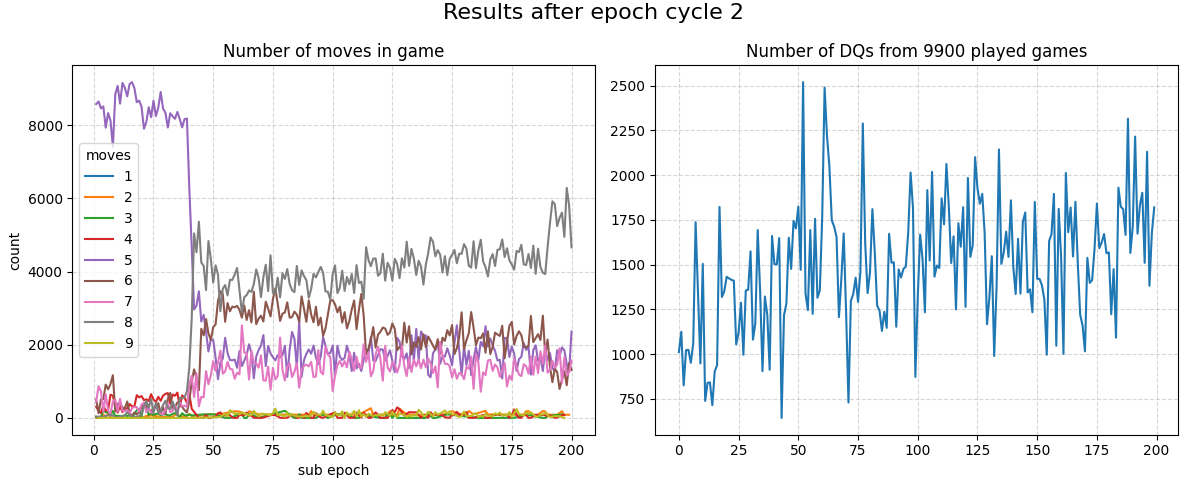Epochs 200-400 the agents are now consistently playing 8-move games!
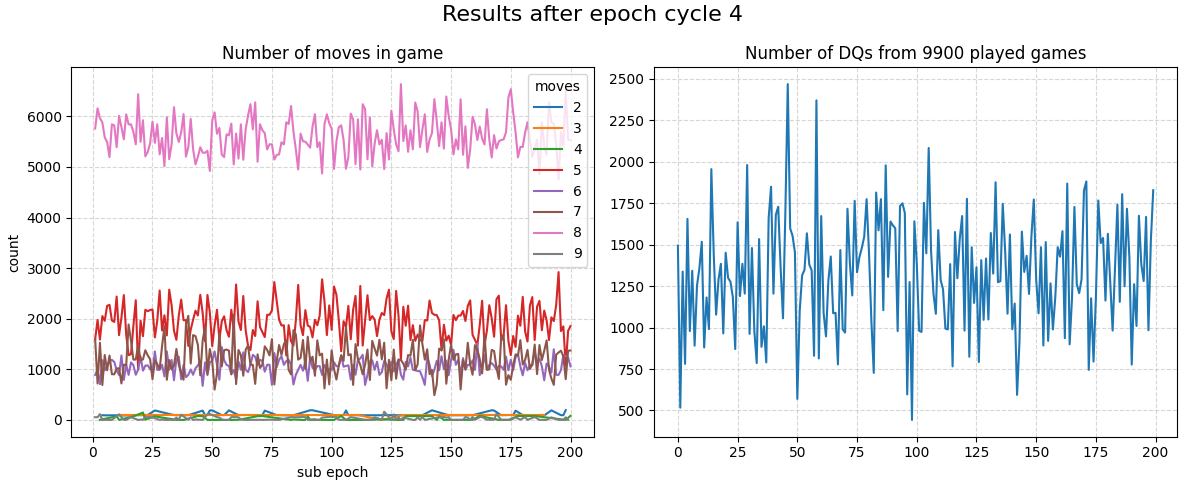Epochs 600-800 there are no longer any 1-move games.
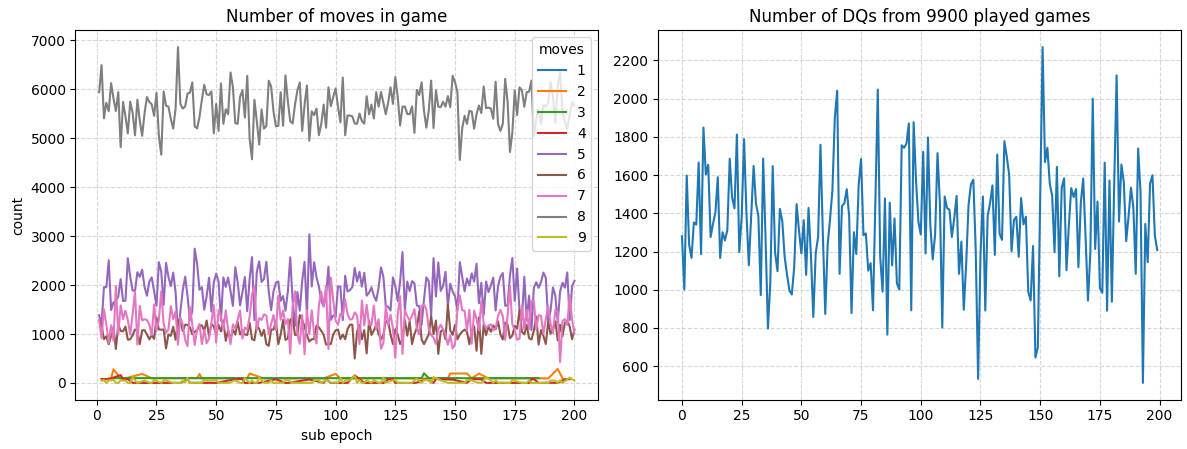The results from epochs 1200-1400 looks the same.
Conclusion and key parameters
This feels like a good place to stop for now. Without any prior knowledge, I was able to make a neural network play mostly valid tic-tac-toe games. I’ll read more about evolutionary algorithms and I’ll definitely improve this project. I have a feeling the most key parameters for this will be:
- The neural network shape (layers and numbers of neurons)
- The mutation amounts of the weights and biases
- The population size
- The number of units that progress each epoch